什么是霍夫曼编码(Huffman Coding)
本文翻译自:What is Huffman Coding?
什么是哈夫曼编码
霍夫曼编码算法是许多压缩算法的基石,如DEFLATE,它被用于PNG格式的图像和GZIP。
为什么需要关注它
你是否也曾想了解:
- 如何在不丢失数据的情况下,对数据进行压缩?
- 为什么某些数据的压缩效果要比其他数据的效果好?
- GZIP如何工作?
5分钟内了解它
假设我们需要压缩一个字符串(哈夫曼编码可以用于任何数据,但是字符串更好理解)。
在被压缩的文本中,一些字符出现的频率总是比其他字符的高。霍夫曼编码利用这一事实,使得最常用的字符比不常用的字符占用更少的空间。
编码字符串
我们要编码的字符串引自Yoda说的话do or do not

do or do not的长度为12个字符。它有一些重复的字符,应该能够被很好的压缩。
为了便于讨论,我们假设存储每个字符占用8bits(字符编码是另外一个话题)。这个句子共占用96个bits,使用霍夫曼编码我们可以做的更好。
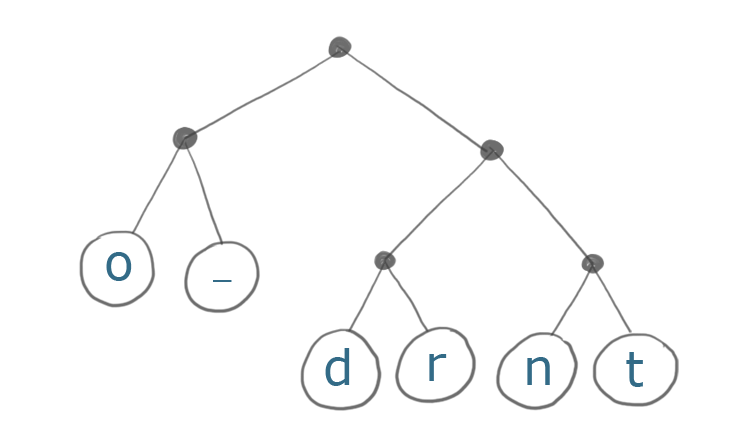
首先我们创建一个树结构。我们的字符串中最常见的字符距树的根节点更近,最少见字符距离根节点更远。
最常见的字符是o(出现了4次)和_(空格,出现了3次)。注意从根节点到这些字符的距离只需要两步,而’t’字符到根节点的距离是3步。
现在,我们可以存储字符的路径来代替存储字符本身。
我们从根节点开始,沿着树向下查找需要编码的字符。如果沿着左边的路径存0,沿着右边的路径存1。
下图是如何使用这颗树来编码第一个字符d: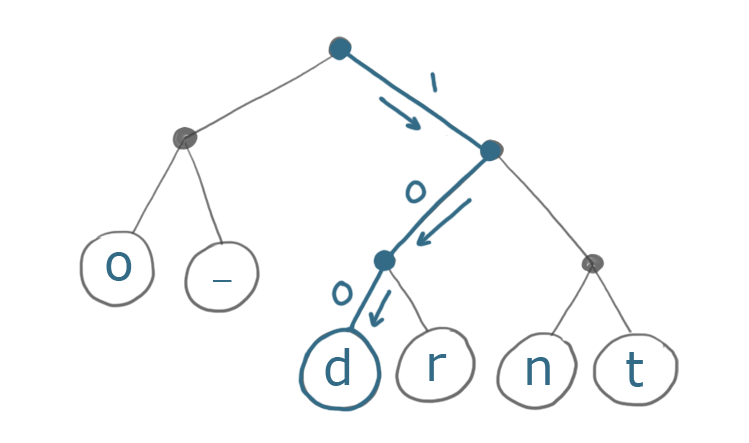
结果是100,3bit代替了8bit。很大的进步。编码后完整的字符串是:
我们用29个bit代替了96个bit,并且没有数据丢失。很棒!
解码字符串
为了解码字符串,我们只需要沿着每一个0(左侧分支)或者1(右侧分支)在从树的根节点开始查找,直到找到到达最后一个字符为止(没有子节点)。
发送已编码的文本
等等…当我们发送已经编码的文本给别人的时候,他们需要这个树吗?是的。为了正确解码字符串,对方需要同样的霍夫曼树。
最简单但是低效的方法是,把树和已经压缩的数据一起发送。
我们也可以在树上达成一致,然后在编码和解码任意字符串的时候使用同样的树。当我们可以提前预测字符的分布时,可以建立一个相对有效的树,而不需要首先看到我们要编码的特定事物(例如,我们可以对英语文本进行编码)
另一个选择是发送足够的信息,让另一方构建与我们相同的树(这就是GZIP的工作方式)。例如,我们可以发送每个字符出现的总次数。但是我们必须小心,对于相同的文本块,可能存在不止一棵Huffman树,所以我们必须确保我们都以完全相同的方式构建树。